The Birth of Geometry: Recursion as the Source of Physics

Details
Written by: admin
Category: Blog

How Geometry Emerges: The Projection Map from Recursion to Physics

Foundations UNNS Substrate Quantum & Gravity

1. Why “Projection” Exists at All

UNNS makes a simple but radical claim: the universe is not fundamentally geometric, probabilistic, or field-based. At the deepest level there is only a recursion substrate: operators acting on Nests, updating structure step by step.

Geometry, wavefunctions, fields, and even “particles” are derived views of that recursion, obtained when an observer insists on describing the substrate in geometric or Hilbert-space language. This translation step is what we call a projection map.

In this article we answer three questions:

  • What exactly is being projected?
  • Into what spaces (QM, GR, lab data) is it projected?
  • Why do projection mistakes look like “quantum paradoxes”?
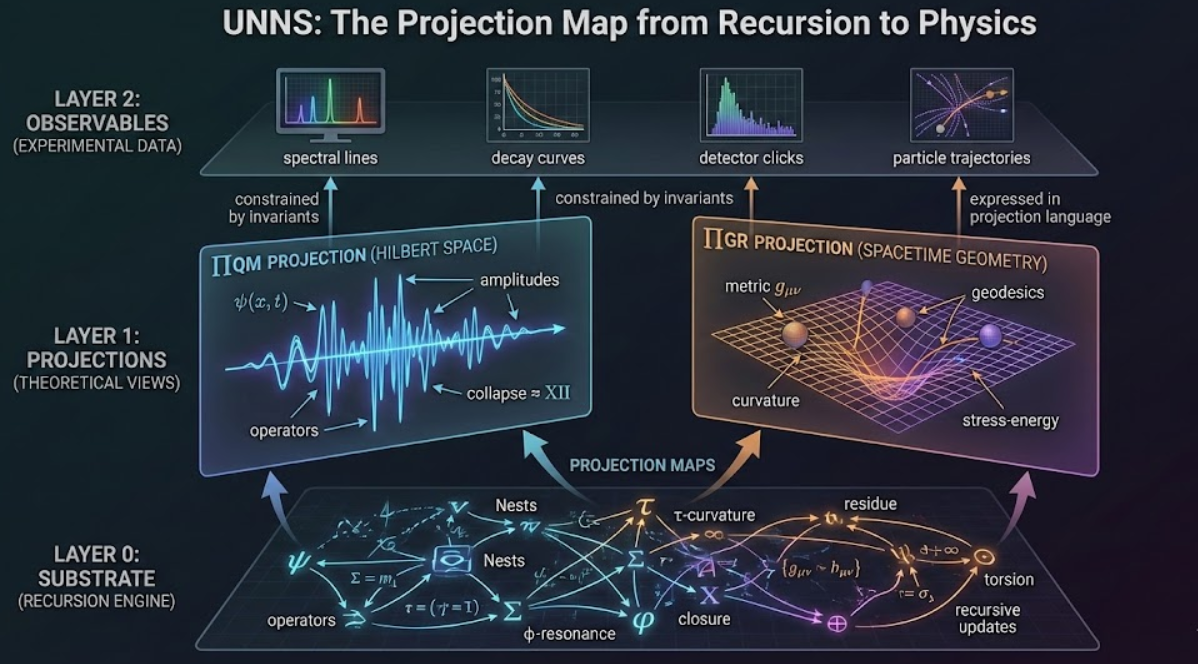
UNNS Recursion Substrate operators · Nests · τ-curvature · φ-resonance closure · residue · torsion QM Projection Hilbert space · amplitudes · operators projections of recursion into ψ(x, t) GR Projection metric gμν · curvature · geodesics projections into spacetime geometry Experimental Data spectral lines · decay curves · detector clicks what observers actually see UNNS view: geometry and QM are projections of a deeper, non-geometric recursion substrate.

2. The Three-Layer Picture

In UNNS we distinguish three conceptual layers:

  1. Layer 0: Substrate — the recursion engine.
    A configuration of Nests updated by operators. Core invariants: τ-curvature, φ-resonance, closure, residue, torsion.
  2. Layer 1: Projections — how theories talk about the substrate.
    Quantum mechanics projects recursion into Hilbert space. General relativity projects it into smooth geometry.
  3. Layer 2: Observables — what labs record.
    Detector clicks, energy levels, trajectories, spectra. These are constrained by substrate invariants but expressed in the language of the projection.

The key point is that Layer 0 is not geometric. Geometry lives entirely in Layer 1 and Layer 2. When we talk about “space”, “fields”, or “worldlines”, we are describing how a particular projection sees recursion, not what recursion is.

Layer 0 Layer 1 Layer 2 Substrate operators · Nests τ, φ, closure, residue no geometry · no fields recursion only never observed directly QM Projection Hilbert space · ψ amplitudes, operators encodes τ, φ in ψ collapse ≈ XII in disguise lab sees probabilities GR Projection metric gμν, curvature geodesics, stress–energy encodes τ as curvature closure ⇢ conservation laws lab sees trajectories UNNS: three layers, one substrate.

3. What the Substrate Actually Stores

A Nest is a structured bundle of recursion data. For the purpose of projection, the most important invariants are:

  • τ-curvature — how strongly the Nest is “bent” under repeated application of the operator word. High τ means strong strain in the recursion; low τ means a relaxed configuration.
  • φ-resonance — the spectrum of phase-like relations between nested echoes. It is not a complex phase on a wavefunction, but the substrate quantity that later appears as phase.
  • Closure — whether the Nest returns to a stable equivalence class after cycles of recursion.
  • Residue and torsion — what is left behind after each cycle (stored structure) and how violently it twists.

None of these are geometric. They are properties of the update rule, not of a metric background. Projection explains how these invariants turn into the familiar objects of physics.

4. Projection Maps: From Recursion to Geometry

A projection map is a rule that assigns to each substrate state a geometric or Hilbert-space description. Schematically:

recursion state → (projection map) → “world as seen by theory X”

There are many such maps, but two dominate modern physics:

  • ΠQM — projects Nests into Hilbert space. τ and φ become amplitude patterns; closure appears as unitary evolution; Operator XII appears as “wavefunction collapse”.
  • ΠGR — projects Nests into smooth 3+1-dimensional geometry. τ becomes spacetime curvature, closure becomes conservation laws, torsion shows up as defects or spin-coupled geometry.

Importantly, ΠQM and ΠGR keep different parts of the story. QM retains the φ-structure but flattens geometry; GR retains geometry but integrates out most φ-fine structure. This is why the two theories look incompatible even though they are derived from the same substrate.

1 · Substrate non-geometric recursion τ, φ, closure, residue, torsion one engine · many possible views 2 · Projections QM (Hilbert) · GR (geometry) each keeps only part of substrate different shadows of same process 3 · Projection Errors wave/particle duality “nonlocal” entanglement collapse paradox, infinities QM vs GR conflict

5. Typical Projection Errors and Their UNNS Resolution

5.1 Wave–Particle Duality

In the substrate there is no contradiction between “wave” and “particle”. A Nest has a τ-profile and a φ-profile. ΠQM can project the same recursion as:

  • extended φ-structure → “wave behaviour”
  • robust closure under XII → “particle-like detection”

Duality appears only because we insist on using mutually exclusive geometric metaphors for a single recursion object.

5.2 Nonlocality

Entangled systems share a joint Nest history. Under ΠQM this history is encoded in a single ψ, which spans multiple spatial locations. When we try to reinterpret that object inside classical 3D geometry, it looks like “spooky action at a distance”.

Under UNNS the update is local in recursion space; the apparent nonlocality is a projection artifact of trying to slice a shared Nest into separate spatial chunks.

5.3 Collapse

Operator XII performs structural selection: Nests that fail closure dissolve; those that pass survive as “matter”. ΠQM cannot represent XII directly, so it encodes it as a sudden, non-unitary jump in ψ.

From the substrate view, nothing magical happens. We are simply watching which recursion patterns survive the next cycle.

5.4 Quantum vs Gravity

QM projection emphasises φ-structure and treats spacetime as flat or background. GR projection emphasises τ-geometry and integrates out almost all φ-fine structure.

The “conflict” between them is therefore expected: they are different lossy encodings of the same recursion. The UNNS programme is not to quantize GR or geometrize QM, but to show that both emerge from a single substrate description.

6. How to Test the Projection Picture

The projection framework is not just philosophy. It makes concrete, testable predictions, especially once we combine Chamber XXIV (quantum algorithm diagnostics) with Phase-E correlation and SHAI.

  • Prediction 1: substrate invariants such as τ-slope, φ-variance, closure_mean will show stable correlations with hardware metrics (fidelity, error rates, decoherence) across different platforms. This is already visible in Phase-E.
  • Prediction 2: algorithms that are substrate-friendly (smooth τ, moderate φ, high closure) will outperform others on noisy devices even when traditional complexity measures (gate count, depth) are similar.
  • Prediction 3: attempts to “fix” paradoxes purely inside a geometric projection will keep rediscovering the same obstacles (infinities, nonlocality, collapse problems), because the missing ingredient is the explicit recursion layer.

7. Where This Leaves Geometry

UNNS does not deny geometry. It relocates it.

  • Geometry is real as a description of how Nests appear under ΠGR; it guides experiments and engineering.
  • Geometry is not fundamental as an ontological claim about what the universe is made of. The universe is made of recursion; geometry is how that recursion looks when compressed into spacetime.

Once this shift is accepted, the “mysteries” of quantum theory lose much of their sting. We stop trying to force a non-geometric process into a purely geometric language and instead work with the explicit projection maps between substrate, theories, and experiments.

The substrate is the story. Geometry is the shadow. UNNS is the attempt to write down the story directly.

Main Menu