Beyond the Barrier: Why Tunneling Occurs in the UNNS Substrate
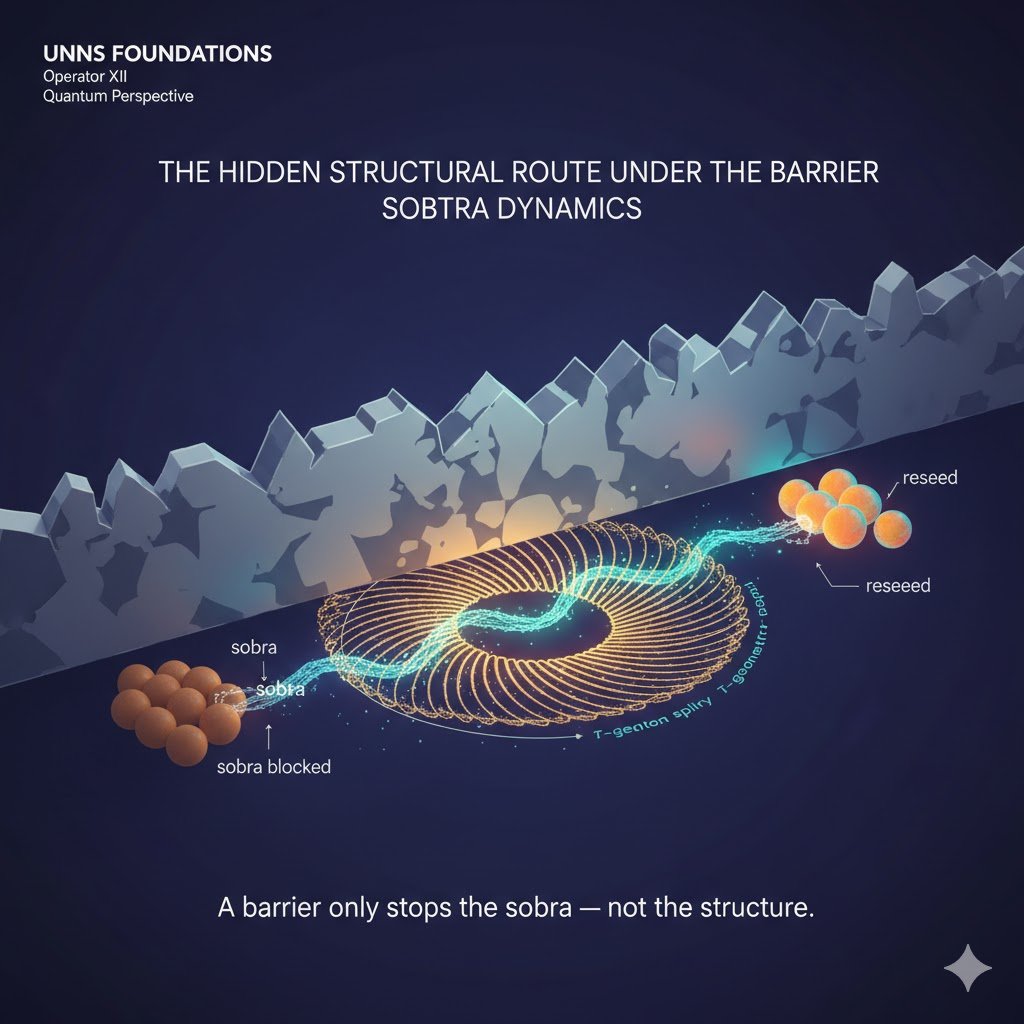
In UNNS, a barrier doesn’t stop a structure — it only stops the sobra. When Collapse selects the sobtra channel, the residue follows a torsion-driven micro-route that bypasses classical geometry entirely. This is the structural origin of tunneling.
1. Introduction — Why Barriers Fail in UNNS
Classical physics treats barriers as absolute limits. Quantum mechanics weakens that limit, allowing “tunneling” — particles appearing on the far side without crossing the middle.
In the UNNS substrate, there is no mystery:
Sobtra is a torsion-reactivated residue capable of transport through τ-geometry, not classical space. This creates a hidden route beneath the barrier.
2. Sobra vs Sobtra — Two Residue Forms
- sobra — inert, curvature-damped echo (no transport)
- sobtra — torsion-reactivated residue (transport channel)
Formally:
$$ S_0(R) = \text{sobra}, \qquad S_{\tau}(R) = \text{sobtra}. $$Operator XII chooses the residue based on torsion vs damping:
$$ \tau(R) > \delta(R) \quad\Rightarrow\quad S_{\tau}(R) \text{ (transport)}. $$3. Torsion Spiral — Lifting the Residue
Torsion does not simply “add energy” — it twists the echo shell, lifting the residue from an inert sobra state into a transport-capable sobtra state. The torsion spiral below shows this lifting action in the τ-layer.
Once lifted along the torsion spiral, the residue is no longer confined to the local curvature basin and can participate in transport — the essential precondition for tunneling-like behaviour.
4. The Hidden Route Beneath the Barrier
The next diagram shows how sobtra bypasses a classical barrier:
The residue does not pass through the barrier. It simply moves along a torsion micro-layer where the barrier does not exist.
5. Structural Interpretation of Tunneling
| Quantum Mechanics | UNNS Interpretation |
| Amplitude under barrier | Echo phase in recursion |
| Tunneling probability | Torsion–damping inequality |
| Particle appears elsewhere | Sobtra reseeds recursion remotely |
6. Collapse → Sobtra → Reseeding
$$ R \xrightarrow{\text{collapse}} S_{\tau}(R) \ \xrightarrow{\text{translation}}\ S_{\tau} \ \xrightarrow{\text{reseeding}}\ R'. $$Sobtra does not tunnel through the barrier — it moves in a domain where the barrier is irrelevant. Thus tunneling is no longer mysterious: it's a choice of collapse channel.
7. Formal Connection to Residue Dynamics Theory
This article gives the conceptual explanation. The full operator analysis, τ-geometry, and commutator structure are presented in the formal paper:
8. Conclusion
Sobtra dynamics reveal a key principle of the UNNS substrate:
When Collapse routes the residue through the sobtra channel, a hidden structural path opens — giving a deterministic substrate explanation for quantum tunneling.
Residue Dynamics and Collapse Channels in the UNNS Substrate:Sobra, Sobtra, and Operator XII as an Evolution Operator
Operator XII is the terminal and generative operator of the UNNS recursive substrate. It receives an arbitrary recursive structure R, extracts its asymptotic echo (sobra), optionally reactivates that echo through torsion (sobtra), and reduces the resulting geometric residue into a new seed from which recursion restarts.
Read the Paper →