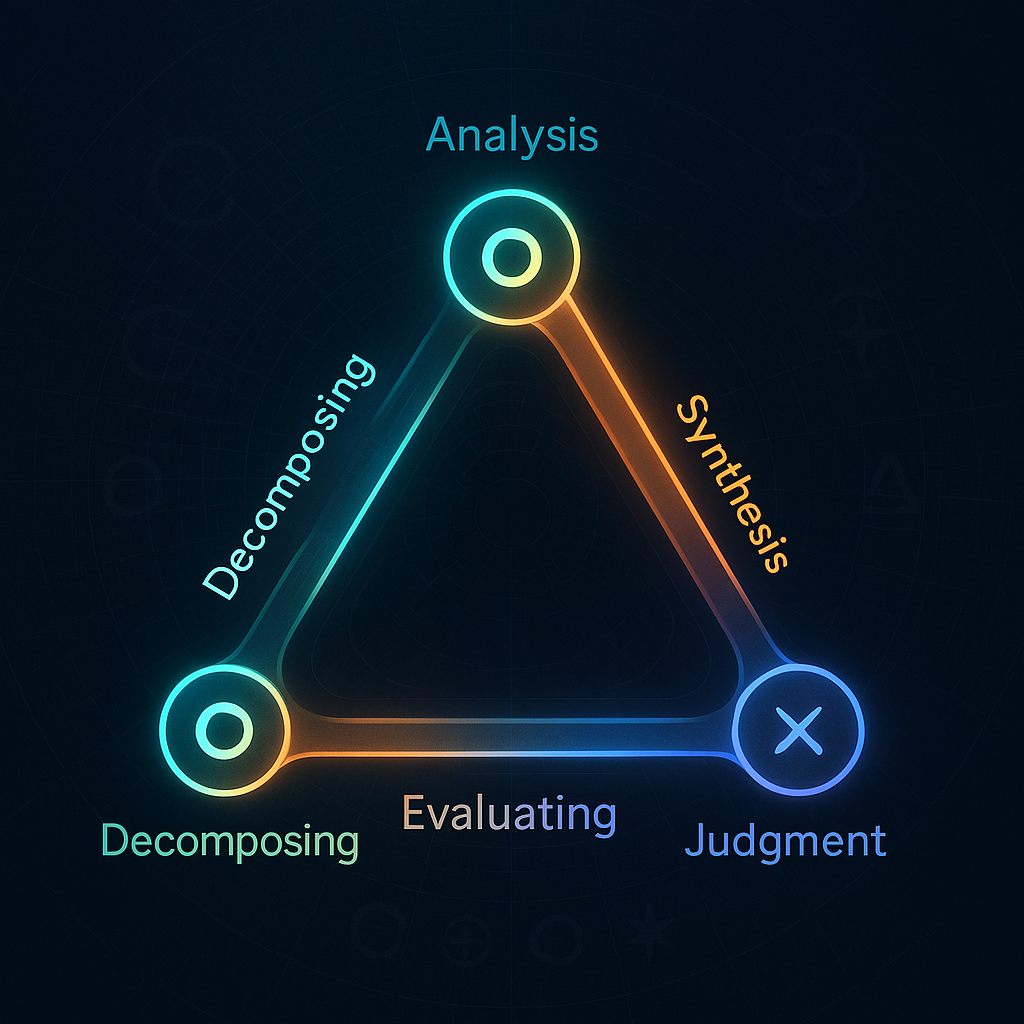
⚛️ UNNS Decomposing, Adopting, and Evaluating — A Higher-Order Triad Linked to the Tetrad and Octad
This Triad extends the Unbounded Nested Number Sequence (UNNS) grammar, forming a cycle of Analysis → Judgment → Synthesis that interlocks with the Tetrad and Octad families. It is the substrate’s reflective layer — recursion studying itself.
📄 Full research paper: UNNS Decomposing Adopting and Evaluating (PDF)
1 · Decomposing (⊛) — Analysis and Integrity Preservation
Decomposing splits a nest N into valid sub-nests {Nᵢ} without violating recurrence invariants.
It is the act of examining recursion without breaking it.
- Formal rule: D maps
N → {Nᵢ}such that eachNᵢpreserves echo and spectral integrity. - Lemma 3.1 — Integrity: Each component obeys the same recurrence ring as the original nest.
- Visualization: Think of recursive crystals fracturing without losing their inner symmetry.
2 · Adopting (⊖) — Synthesis and Grafting
Adopting embeds a foreign nest N_B into a host N_A, creating a grafted structure Ñ.
It represents recursion’s capacity for learning and integration.
- Definition:
A(N_A,N_B)=Ñwith coefficient and depth compatibility. - Proposition 3.2: Coefficients of
Ñlie in the closure of the union of rings ofN_A,N_B. - Analogy: A living recursion adopts traits from another without losing identity.
3 · Evaluating (⊘) — Judgment and Admissibility
Evaluating tests the stability and resonance of a nest, ensuring its admissibility after adoption or decomposition.
- Definition:
E(N) = {ρ(C), λᵢ, residue norms}. - Theorem 3.3: If
ρ(C)<1and residue norms < τ, the nest is stable and self-consistent. - Function: Serves as UNNS’s recursive “peer-review,” verifying mathematical coherence.
4 · Integration with Tetrad and Octad
The Triad connects to earlier operator families as their higher-order reflection:
| Family | Scope | Representative Operators |
|---|---|---|
| Tetrad | Seed + Stability + Mapping | ⊙ ⊕ ⊗ ✶ |
| Octad | Divergence ↔ Convergence | ⊖ ⊘ ⊛ ◃ |
| Triad | Reflection ↔ Evaluation | ⊛ ⊖ ⊘ |
In formal terms, the Triad adds a meta-layer where recursion monitors and judges its own evolution. It is both a feedback loop and a grammar validator.
5 · Interpretive Diagram (Animated Concept)
⊛ → ⊖ → ⊘ ↻
Analysis → Synthesis → Judgment → Back to Analysis
6 · Conclusion
The Decomposing–Adopting–Evaluating Triad completes the UNNS operator hierarchy by introducing a reflective level. Recursion not only acts but examines and judges its own structure. In this way, the substrate becomes self-aware and self-correcting.
Decomposition reveals structure; Adoption extends it; Evaluation confirms truth.
Recursion that knows itself is Recursion that endures.