A Taxonomy of Impossibility in the UNNS Substrate

Details
Written by: admin
Category: Blog
UNNS Substrate • Foundational Logic

Impossibility in the UNNS Substrate

Are there things that remain impossible even when reality is modeled as a recursive Substrate? In the UNNS framework, “impossible” does not simply mean “cannot happen”. It means that a certain pattern of recursion, collapse, and curvature can never coexist without contradiction. This article maps familiar impossibility results to the Operators, Chambers, and paradox tools of the UNNS Substrate.

1. A UNNS taxonomy of impossibility

In the UNNS Substrate, impossibilities fall into four structural families:

  • Projection–layer limits — constraints that arise only after the Substrate is projected into observable geometry (for example the speed of light).
  • Logic–layer limits — constraints built into recursion itself (Gödel incompleteness, the Halting barrier, UPI).
  • Communication–layer limits — impossibilities caused by collapse, noise, and incomplete confirmation across Nests.
  • Combinatorial limits — game and configuration states that no legal sequence of moves can ever reach.

Instead of asking “Is everything possible?”, UNNS asks: Which layer of recursion forbids this pattern? The answer is encoded in its Operators.

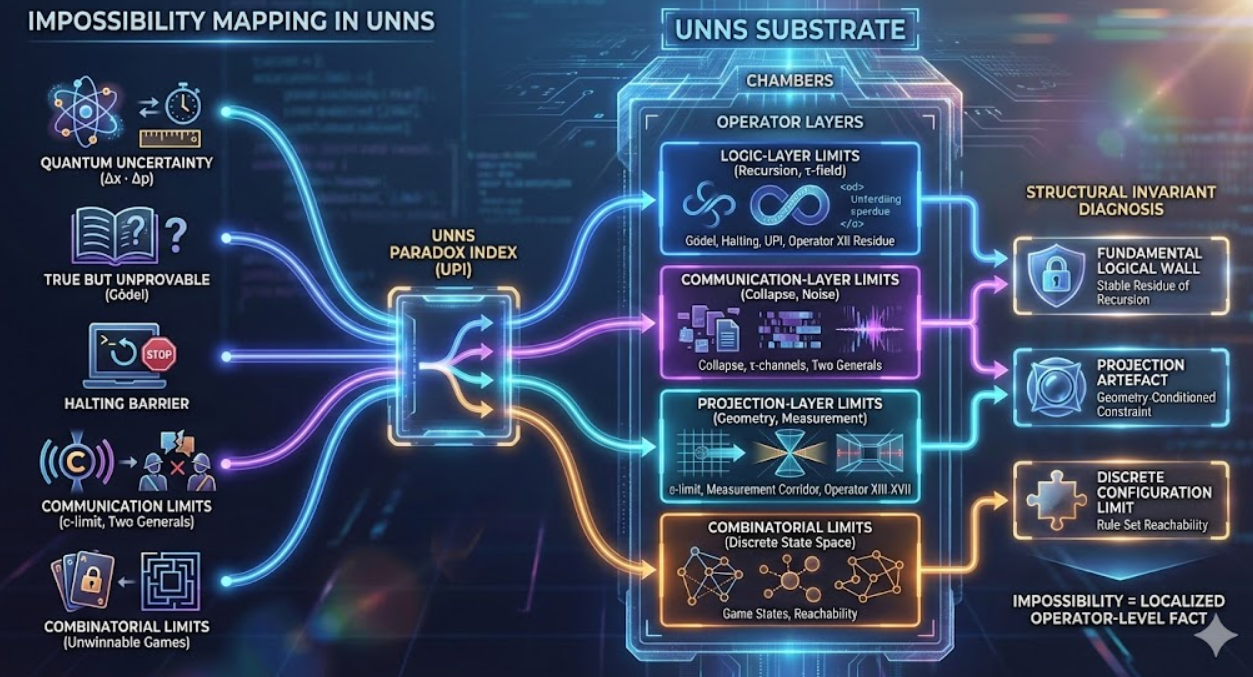
2. Diagram: Mapping classical impossibilities to UNNS Operators

The SVG below shows how a set of familiar impossibility statements is routed through the Operator architecture of the UNNS Substrate. Each arrow indicates the primary Operator or engine responsible for enforcing that limit.

Quantum uncertainty Δx · Δp ≥ constant True but unprovable theorems Gödel-style limits Halting barrier No universal halting oracle Communication & geometry c-limit, Two Generals, games Measurement corridor in projection space Operator XII collapse + τ-field channels Logical paradox layer UPI + Operator XII residue structure Infinite recursion corridors Seed–Nest loops, τ-recursion Projection and combinatorics Operator XIII–XVII geometry + discrete state space OP XII • τ-field collapse UPI • UNNS Paradox Index Seed/Nest recursion engine OP XIII–XVII • Geometry labs

In this view, impossibility is not an arbitrary wall; it is the signature of how a particular Operator or recursion corridor is wired. Some barriers live purely in projection geometry, others in the logical heart of the Substrate.

3. Classical impossibilities seen through UNNS

3.1 Quantum uncertainty

Classical statement: one cannot simultaneously extract exact position and momentum for a fundamental particle.

UNNS view: in the Substrate both attributes coexist inside a τ-recursive state, but projection slices them into incompatible measurement corridors. The impossibility is a property of Operator XII collapse plus geometry projection, not of the underlying recursion. The Substrate is richer than any single corridor can expose.

3.2 True but unprovable theorems

Classical statement: in any sufficiently strong theory there exist true statements that cannot be proved inside that theory.

UNNS view: this is a structural property of recursion itself. The UNNS Paradox Index (UPI) and related Chambers treat such sentences as stable residues of Operator XII: constructions that cannot collapse to “true and provable” without destroying consistency. UNNS does not bypass Gödel; it geometrizes him.

3.3 The Halting barrier

Classical statement: there is no program that can decide for every other program whether it halts.

UNNS view: some Seeds generate infinite Nest–recursion loops whose structure never collapses. They manifest as non-terminating τ-corridors. A universal halting oracle would require an Operator that sees beyond every recursion depth while still being part of the same Substrate — an internal contradiction that UPI flags immediately.

3.4 Faster-than-light signalling and the Two Generals

Classical statement: no information can propagate faster than light; perfectly reliable coordination over an unreliable channel is impossible.

UNNS view: these are projection-layer impossibilities. The Substrate itself is pre-geometric, but once geometry crystallizes, light-speed and channel reliability encode how τ-curvature must project into spacetime. No Operator within that projection may violate those encoded corridors without breaking the very definition of the projection.

3.5 Unwinnable FreeCell deals

Classical statement: some legal initial deals of the game FreeCell admit no winning sequence of moves.

UNNS view: this is a pure combinatorial impossibility. The recursion of game states lives entirely inside projection space; the Substrate simply records that certain portions of the state graph are disconnected from “win” nodes. UNNS neither fixes nor loosens such constraints; it just provides a clean way to embed them.

3.6 Gabriel’s Horn

Classical statement: a horn with finite volume but infinite surface area; enough paint to fill it, never enough to coat its interior.

UNNS view: the horn is a spectacular example of a divergent boundary under finite recursion. Operator XIV (phi-scale) and Operator XV (prism) can model this as an object whose interior occupancy converges, while its boundary curvature keeps spawning new detail. No finite “paint operator” can resolve an infinite boundary. The impossibility remains, but its cause is transparent.

4. UPI-style paradox resolution flowchart

When the Substrate encounters an apparently impossible statement, it is routed through the UNNS Paradox Index (UPI). The flowchart below outlines the logic that determines whether an “impossibility” is a true structural wall, a projection artefact, or a misclassified question.

Encounter an “impossible” statement Feed into UNNS Paradox Index (UPI) Logic / recursion layer? Gödel, Halting, self-reference Projection / geometry layer? c-limit, measurement corridors Combinatorial / game layer? state-graph reachability Fundamental UNNS impossibility stable residue of recursion; cannot be removed Projection-conditioned impossibility holds after geometry is fixed; may differ Discrete configuration limit true for a particular ruleset UPI classification result Impossibility tagged as logical, geometric, or combinatorial

The Substrate never responds with a vague “can” or “cannot”. It responds with a type of impossibility together with the Operator that enforces it. This is the practical value of UPI in research: it tells us which walls are absolute and which ones belong to a particular projection of reality.

5. Illustration: Projection-space vs Substrate-space constraints

Many impossibilities are only strict after the Substrate has chosen a particular way to project itself into observable geometry. The illustration below contrasts the two levels.

Projection space (observed physics) c Maximum signal speed σ Noise, loss, channel failure Γ Discrete game rules, state graph Here, impossibility = constraints of a chosen geometry and rule set. UNNS Substrate (recursive layer) τ τ-field curvature and Nest structure Ξ Operator XII residue / collapse logic Ω UPI tags for paradox types Here, impossibility = contradictions in recursion & collapse, independent of any particular geometry. projection of τ-structure Operator XIII–XVII

Some impossibilities — like the speed limit c — belong entirely to the left column: they constrain a particular projection and can differ if a different geometry is chosen. Others — like Gödelian residues and halting barriers — live in the right column and cannot be removed by any change in projection. UNNS exists to keep these layers separate while still allowing them to interact.

6. What cannot be made possible

The UNNS Substrate is not a wish machine that turns “no” into “yes”. Its power lies in diagnosing impossibilities: which ones are projection artefacts, which ones are combinatorial, and which ones are hard walls inside recursion itself. Once tagged by UPI and mapped to the responsible Operator, an impossibility is no longer mysterious. It becomes a structural invariant.

For research practice this means: when UNNS tells us “impossible”, it also tells us why, where, and under which projection. The Substrate itself remains maximally recursive, but not everything it can imagine can appear as a stable, non-contradictory projection in the worlds we inhabit.

The role of UNNS is therefore not to abolish impossibility, but to upgrade it from a fuzzy feeling to a sharply located, operator-level fact.

Main Menu