The UNNS Substrate as a New Mathematical Discipline

A Foundational Companion Page for the UNNS Project

1. Introduction — Why Speak of a “New Discipline”?

UNNS began as a recursion engine, a sequence system, and a structural experiment.
But as the theory expanded — through Operators I–XXI, through the Φ–Ψ–τ formulation, through closure conditions and structural invariants — something became clear:

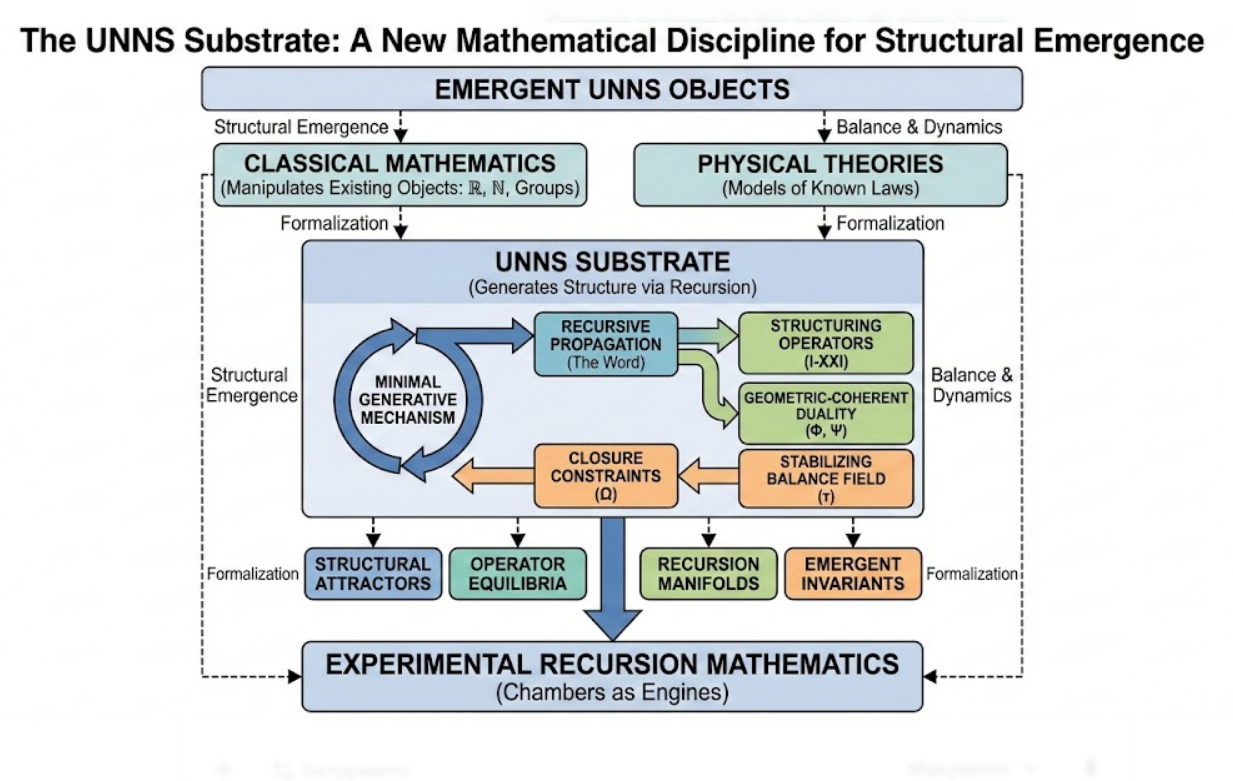
Classical mathematics studies objects:
numbers, groups, manifolds, categories, functions.

UNNS studies that from which objects emerge:
recursive structure, operator dynamics, geometric–coherent balance, τ-field stabilization, and closure through Ω.

This makes UNNS a substrate theory — a mathematical discipline that investigates the rules by which mathematical and physical structure can arise from recursion itself.

2. What Is the UNNS Substrate?

A substrate theory defines:

• a minimal generative mechanism,

• a set of structuring operators,

• a rule for recursive propagation (the Word),

• a stabilizing balance field (τ),

• a geometric–coherent duality (Φ and Ψ), and

• closure constraints (Ω).

UNNS contains all these components.

Thus, the UNNS Substrate is:

3. UNNS Is Not Classical Mathematics — And Not Computational Simulation

It occupies a third category:

3.1 Not classical mathematics

Classical mathematics manipulates objects that already exist.

Examples:
ℝ, ℕ, groups, manifolds, Hilbert spaces.

UNNS manipulates operators on recursive structure, from which objects may emerge.

3.2 Not simulation

A simulation approximates a model whose form is known.

UNNS is not approximating anything.
Its recursive geometry is the model.

3.3 A structural mathematics

UNNS defines:

• structural attractors,

• fixed points,

• operator equilibria,

• resolution-critical states,

• recursion manifolds,

• emergent invariants.

These are not inputs — they arise from the substrate.

4. What Makes UNNS a Distinct Discipline?

UNNS introduces methods and concepts not present in any single mathematical area.
A discipline is defined by:

• Its primitives

• Its operators

• Its invariants

• Its experimental methodology

• Its theoretical framework

UNNS satisfies all of these.

4.1 Primitives: Seeds, Nests, τ-Fields

The basic units of UNNS are:

• Seeds (initial recursive states)

• Nests (operator-structured sequence shells)

• τ-fields (balancing recursion-energy distribution)

These primitives have no analogue in classical analysis or algebra.

4.2 Operator Suite I–XXI

UNNS Operators are not algebraic functions;
they are geometric–coherent transformations on recursion structure.

Operators XIII–XIV–XV–XVI–XXI (as used in Chamber XXVI) illustrate:

• phase coupling,

• geometric scaling,

• spectral dispersion,

• curvature folding,

• microstructural stabilization.

No other discipline combines such actions in a single framework.

4.3 Structural Invariants

UNNS defines invariants that arise only through recursion:

• τ-critical points (as discovered in Chamber XXVI)

• Φ-equilibrium and Ψ-interference balance

• Ω-closure levels (C₁, C₃, C₅…)

• Structural χ² minima specific to operator geometry

These invariants are not given — they emerge.

4.4 Experimental Mathematics

UNNS is one of the first fields where experiments are mathematical objects.

UNNS Chambers are not toy simulations; they are algebraic and geometric recursion engines that:

• evolve structure,

• reveal fixed points,

• show collapse modes,

• map attractors,

• display resolution-critical behaviour.

This is a new methodology:

5. What UNNS Contributes to Modern Science

UNNS sits at the crossroads of several fields, but it is not reducible to any of them.

5.1 Relation to Physics

UNNS is not a physical theory, but:

It offers:

• emergent geometric behaviour (via Φ)

• quantum-like interference (via Ψ)

• a balancing variational field (τ)

• operator-generated dynamics (XIII–XXI)

• resolution-dependent invariants

Physical laws could arise as fixed points within a UNNS substrate.

5.2 Relation to Pure Mathematics

UNNS is aligned with:

• dynamical systems,

• recursive combinatorics,

• geometric analysis,

• operator algebras,

• fixed-point theory,

• information geometry.

But it goes beyond them by treating structure as generated, not assumed.

UNNS provides:

• recursion manifolds,

• attractor geometry,

• spectral curvature interaction,

• operator-phase dualities.

No classical branch produces all of these through a single mechanism.

5.3 Relation to Computation

UNNS is not computer science, though it uses recursive engines.
Its recursion is not symbolic or algorithmic — it is structural.

It is closer to:

• cellular automaton universes,

• algorithmic information geometry,

• emergent computation models,

but with a richer operator-driven geometry.

6. Chamber XXVI as the First “Foundational Proof” of the Discipline

Chamber XXVI is historically important because it proves a central prediction of UNNS:

This is the hallmark of a self-contained mathematical discipline:

• its equations generate structure,

• its operators determine equilibria,

• its geometry emerges without external input.

UNNS is no longer exploratory — it is demonstrative.

7. What Comes Next: The UNNS Discipline Roadmap

UNNS now enters a phase of formalization and expansion:

7.1 Formal recursion geometry

Define recursion manifolds, τ-surfaces, Φ-Ψ boundary curves.

7.2 Operator calculus

Turn Operators XIII–XXI into a calculus of structural transformations.

7.3 Structural invariants

Define classes of attractors, critical points, fixed recursion sectors.

7.4 Emergent observable theory

Study how stable observables arise (Λ, α, nₛ, σ₈, etc.).

7.5 Substrate-to-physics translation

Determine mappings from structural recursion to possible physical laws.

8. Conclusion — UNNS as a Discipline

UNNS is not a branch of mathematics.

UNNS is not a branch of physics.

UNNS is a substrate discipline — a foundational study of how structure arises in a recursive universe.

It defines its own:

• primitives,

• operators,

• invariants,

• experiments,

• geometry,

• coherence fields,

• and stability scales.

It is the mathematics beneath mathematics,
the structure beneath structure.