From Executable Recursion to Structural Invariants

Details
Written by: admin
Category: UNNS Research

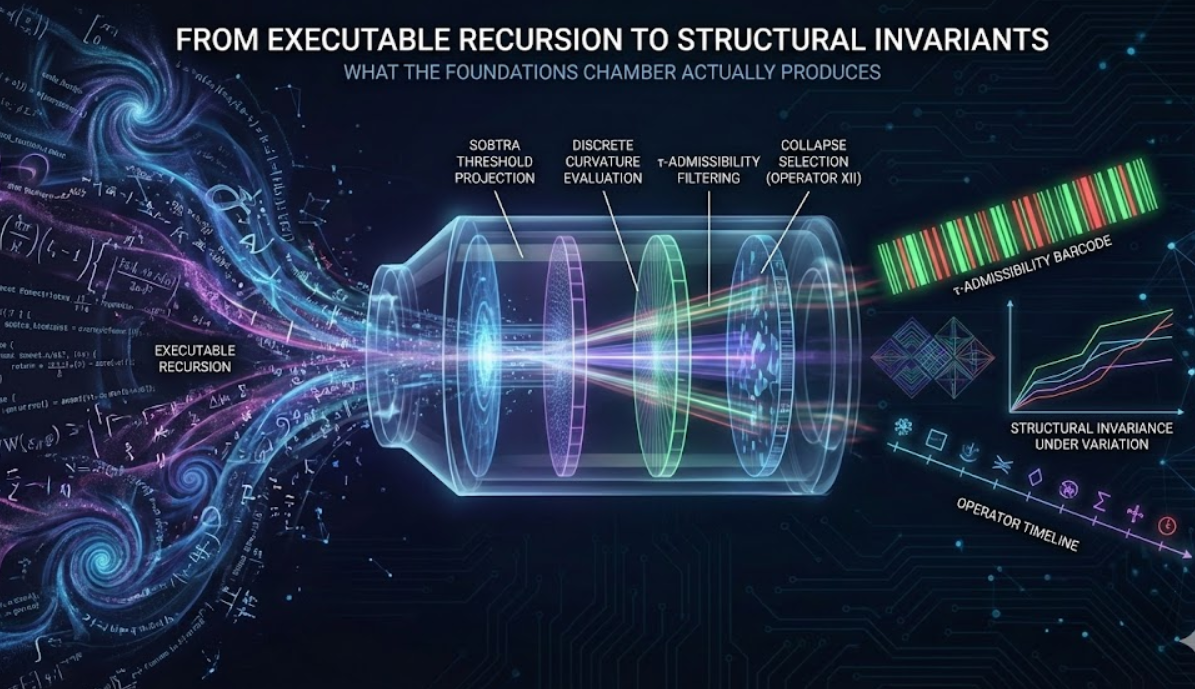
What the Foundations Chamber Actually Produces

Abstract

The UNNS τ-Filtered Observability — Foundations Chamber is not a visualization tool, nor a simulation in the conventional sense. It is an executable instrument designed to extract structural invariants from recursive dynamics under observability constraints.

This article clarifies what kind of results the Chamber produces, how they should be interpreted, and why they are neither numerical constants nor empirical predictions. Instead, the Chamber exposes relations that persist under controlled variation—the defining feature of structural invariants in mathematics and physics alike.

Recursion → Observability → Invariants Recursive State τ-Filtering Structural Invariant

1. What Counts as a Result?

When a run completes in the Foundations Chamber, no single number is presented as “the answer.”
This is intentional.

The primary outputs are structured datasets describing how a recursive process behaves under:

  • Sobtra threshold projection

  • discrete curvature evaluation

  • τ-admissibility filtering

  • collapse selection (Operator XII)

A result, in this context, is not a value, but a pattern that persists across:

  • parameter variation

  • τ-threshold adjustment

  • multi-run comparison

This places the Chamber closer to tools like:

  • phase-space analysis

  • renormalization flow diagrams

  • spectral decompositions

than to numerical solvers.

Observable Layers in Each Run Layer 1: State Trajectory (x₀, x₁, x₂, ...) Layer 2: Sobtra Decomposition (retained + residue) Layer 3: Discrete Curvature (κₙ profile) Layer 4: τ-Admissibility (binary mask) Layer 5: Operator Assignment (Φ, Ψ, τ, XII)

2. Primary Observables Produced by the Chamber

Each execution produces several observable layers. None are optional.

2.1 State Trajectory

The raw recursive sequence
x₀, x₁, x₂, …, xₙ

This is not yet an invariant—it is the substrate on which invariants are extracted.

State Trajectory: xₙ vs n step n state xₙ

2.2 Sobtra Decomposition

Each step is decomposed into:

  • retained component (Sobtra)

  • rejected component (residue)

This separation is structural, not heuristic. It enables the next layer.

Sobtra Decomposition: xₙ = sobtra + residue θ threshold n=1 n=2 n=3 n=4 n=5 n=6 n=7 n=8 sobtra (retained) residue (rejected)

2.3 Discrete Curvature Profile

For each step n, curvature κₙ is computed as:

κₙ = ‖rₙ₊₁ − rₙ‖ / (‖xₙ‖ + ε)

This quantity measures local instability of recursion under projection, not geometric curvature.

The κ-profile over time is a first-order diagnostic of structural stress in the system.

Discrete Curvature: κₙ vs n Λ step n κₙ κ ≤ Λ (admissible) κ > Λ (collapse)

2.4 τ-Admissibility Mask

A step is admissible if:

κₙ ≤ Λ

This produces a binary admissibility sequence that partitions the run into:

  • τ-stable segments

  • collapse-triggering segments

This mask is one of the Chamber’s most important outputs.

τ-Admissibility Barcode 0 20 50 80 100 τ-admissible (κ ≤ Λ) collapse (κ > Λ)

2.5 Operator Assignment

Each step is labeled according to its local behavior:

  • Φ (growth-aligned)

  • Ψ (rebalancing)

  • τ (stable continuation)

  • XII (collapse)

The operator timeline is derived, not assumed.

Operator Timeline Φ Φ τ τ XII Ψ τ XII τ τ Φ growth Ψ rebalance τ stable XII collapse

3. What Makes an Invariant?

An invariant in the Foundations Chamber is anything that survives structured variation.

Examples:

  • Survival ratio remains stable across Λ adjustments

  • Collapse locations align across multiple runs

  • Operator dominance patterns persist under noise changes

  • Path persistence remains constant in comparison mode

None of these are single values.
They are relations that do not disappear when conditions change.

Structural Invariance Under Variation Λ = 0.05 Λ = 0.08 Λ = 0.12 Survival: 0.54 Survival: 0.68 Survival: 0.79 Survival ratio increases monotonically with Λ This relation is INVARIANT Exact collapse locations vary (contingent) But the monotonic trend persists (structural)

4. Why These Are Not Numerical Constants

The Chamber deliberately does not output universal constants.

Why?

Because:

  • constants depend on scale, normalization, and units

  • UNNS analysis operates on structural relations, not measurement scales

Instead, the Chamber identifies:

  • invariant proportions

  • stable classifications

  • persistent structural transitions

This is analogous to how:

  • critical exponents matter more than raw values

  • universality classes matter more than parameters

Relations vs Constants Not Universal Constants κ = 0.0623 ✗ Structural Relations survival ∝ Λ collapse ~ κ > Λ ✓ Scale-dependent • Unit-sensitive • Normalization-variant • Context-specific Scale-invariant • Proportional • Classification-stable • Comparison-persistent

5. Multi-Run Comparison as a Test of Invariance

The Compare tab performs a specific task:

It tests whether structural features persist across independently generated runs.

What is compared:

  • admissibility overlap

  • survival ratios

  • collapse alignment

  • operator frequency stability

If a feature survives comparison, it qualifies as structural.

If it disappears, it is classified as contingent.

This distinction is the core contribution of the Chamber.

Multi-Run Comparison: Survival Stability Test Run 1 (seed 1234) 63% Run 2 (seed 5678) 61% Run 3 (seed 9012) 62% Overlap regions show structural persistence Survival ratio: 62% ± 1% (stable) | Alignment: 74% (structural)

6. How to Read the Exported JSON

The exported JSON files are not logs—they are analysis objects.

Recommended workflow:

  1. Identify admissibility mask

  2. Locate collapse indices

  3. Examine κ-distribution

  4. Track operator transitions

  5. Compare across runs

The included files:

  • test_run_valid.json

  • test_run_comparison.json

provide reference baselines for this process.

JSON Export Structure { "schema": "UNNS_FOUNDATIONS_RUN/v1", "run_id": "test-run-002", "config": { lambda, delta, noise, ... } "steps": [ { n, x, sobtra, residue, kappa, ← Curvature measure admissible, ← τ-mask (binary) ] }

7. Why This Matters

Many mathematical and physical systems produce large amounts of data but few invariants.

The Foundations Chamber reverses this:

  • it restricts observability

  • enforces admissibility

  • treats collapse as structural

  • compares survival, not values

What remains are facts about structure, not interpretations.

From Data Deluge to Structural Facts Typical System High data volume Few invariants τ-filtering Foundations Chamber Reduced observables Clear invariants

8. Summary

The Foundations Chamber does not answer what a system is.
It answers what survives.

Those survivals—when consistent, reproducible, and comparison-stable—are structural invariants.

This is the kind of fact the Chamber is designed to produce.

The Chamber's Answer "What is the system?" "What survives?" ✓

Resources

Primary Materials


Test Data

Main Menu