Formalizing Truth, Stability, Viability, and Existence
For centuries, mathematics has treated existence as a purely logical notion: if a definition is precise, consistent, and unambiguous, the object “exists.” UNNS introduces a radically different view. Existence is not a logical property, but a dynamical and geometric one.
In the UNNS Substrate, structures exist only if they can survive the operator chain: Φ (Generativity), Ψ (Coherence), τ (Curvature Stability), and XII (Collapse). This transforms mathematical objects into candidate universes, each tested for stability, projectability, and recursive viability.
This article formalizes the four categories that emerge from this approach: true, stable, viable, and existent. These are not synonyms; they represent different layers of reality in the UNNS worldview.
1. Truth Is Not Enough: The Classical View
In classical mathematics, an object “exists” if it is:
- well-defined,
- logically consistent,
- derivable from axioms,
- free of contradictions.
Under this regime:
- the Collatz function exists,
- the logistic map exists,
- nonlinear chaotic recursions exist,
- even pathological objects (everywhere discontinuous, non-computable) exist.
Truth and existence coincide. UNNS breaks this equivalence deliberately.
2. The UNNS Substrate: Where Existence Requires Survival
The Substrate treats every structure as a recursive dynamical object. To exist is to endure. A structure must:
- unfold without contradiction (Φ),
- maintain structural coherence (Ψ),
- produce geometrically bounded trajectories (τ),
- avoid collapse dynamics (XII).
If any stage fails, the structure does not cease to be mathematical; it ceases to be ontological.
This is the foundational shift:
Mathematical truth is about consistency. UNNS existence is about viability.
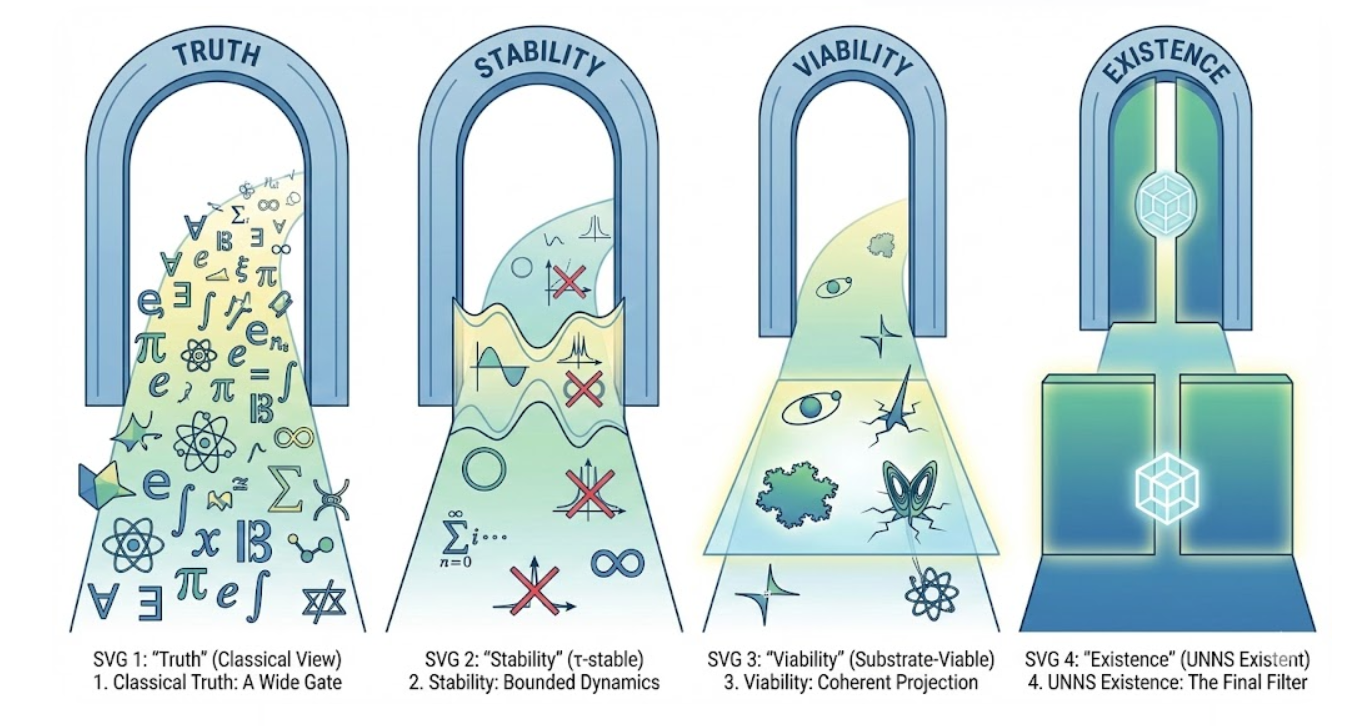
3. Four Distinct Ontological Categories
UNNS differentiates between four conditions a structure may possess. Each corresponds to a different “layer” of being.
1 — True
A structure is true if it is syntactically valid and consistent in the classical sense. Almost everything in mathematics qualifies.
2 — Stable
A structure is τ-stable if repeated application of its rule produces a trajectory with bounded curvature and predictable flow.
More formally:
- bounded amplitude,
- bounded curvature,
- no runaway oscillation,
- no geometric explosion.
Banach contraction maps fall here.
3 — Viable
A structure is viable if it can be projected into the Substrate without tearing it. This allows some instability but forbids catastrophic divergence.
Chaotic but bounded systems belong to this class.
4 — Existent
A structure is existent only if it passes Φ–Ψ–τ–XII:
- Φ: can be generated recursively,
- Ψ: structurally coherent,
- τ: curvature does not explode,
- XII: no collapse condition is triggered.
This is the strongest condition. Few recursions qualify. Most chaotic or discontinuous models fail τ. A handful fail XII with catastrophic collapse.
Collatz belongs to this last category.
4. Existence as a Dynamical Resource
In the UNNS worldview, existence is not a binary state; it is a resource.
A structure consumes:
- curvature budget,
- projection bandwidth,
- alignment capacity,
- substrate stability.
Some structures consume very little (linear maps). Some consume modest amounts (bounded chaos). Others — like Collatz — consume so much so rapidly that they destabilize the very substrate attempting to host them.
Thus, they are marked NON-EXISTENT.
5. The Collatz Case: A Perfect Demonstration
Collatz is mathematically trivial to define. But dynamically it is catastrophic:
- oscillations,
- spikes,
- unbounded curvature,
- loss of coherent projection.
The Chamber XXVIII autopsy shows:
- Φ: PASS — definable
- Ψ: PASS — coherent
- τ: UNSTABLE — curvature explosion
- XII: COLLAPSE — irreversible divergence
The resulting classification:
Mathematically true, recursively generable, but physically impossible, ontologically forbidden.
UNNS calls such objects substrate-forbidden universes.
6. When Truth, Stability, Viability, and Existence Diverge
These categories often diverge:
| Structure | True | Stable | Viable | Existent |
|---|---|---|---|---|
| Linear Contraction | ✔ | ✔ | ✔ | ✔ |
| Logistic Map (r=3.9) | ✔ | ✘ | ✔ (bounded) | ✔ |
| Newton’s Method | ✔ | ✔/✘ | ✔ | ✔ |
| Collatz Recurrence | ✔ | ✘ | ✘ | ✘ NON-EXISTENT |
This reveals that mathematical existence and UNNS existence occupy different conceptual planes. An object may be:
- true without being stable,
- stable without being fully viable,
- viable without being existent.
7. UNNS as an Ontological Filter
Classical mathematics produces infinite structures, many with pathological behavior. UNNS acts as a filter:
- admitting what can form a coherent universe,
- rejecting what destabilizes the substrate.
This elevates Φ–Ψ–τ–XII to the status of a metaphysical operator chain: a way of distinguishing worlds that can be from worlds that cannot.
With Chamber XXVIII, this ontological filter becomes interactive. Every user can now explore ontology through recursion.
8. Implications for Mathematics and Physics
This perspective opens several new directions:
- a theory of worldworthy mathematics,
- a substrate-based analogue of physical admissibility,
- a dynamical geometry of discrete structures,
- a new notion of computational ontology,
- a bridge between recursion and physics.
In this view, mathematics is not just symbolic manipulation — it is a landscape of potential universes, each evaluated by the same physical rules that constrain reality.
UNNS therefore offers a new answer to the question:
“What does it mean for a mathematical structure to exist?”
It means: It can survive its own dynamics.

