Why the Dirac Delta Survives in Mathematics but Not in Dynamics

Details
Written by: admin
Category: UNNS Research

Separating definition power from survival under evolution

A UNNS foundations lens: δ(x) is structurally valid as a limit-object, yet it fails τ-admissibility as a runtime state. This article separates “definition power” from “survival under evolution” using κ-curvature, Λ thresholds, and Collapse (XII).

Topic Distributions & stability Lens τ-filter + κ Operator XII (Collapse) Output Regimes (stable / critical / collapse)

1) The two places δ lives

In classical analysis, δ is a distribution: it is defined by how it acts under integration against test functions. In dynamics, δ behaves like an “infinite localization” target. UNNS treats these as two different questions: What can be defined? versus What can survive as an evolving object?

Mathematics (distribution definition)
∫ f(x) δ(x − a) dx = f(a)

UNNS translation

  • δ as a definition: an evaluation rule (a valid mapping on a test space).
  • δ as a state: an attempted runtime configuration with extreme concentration.
  • UNNS distinction: “well-defined” does not imply “τ-admissible.”

Quick classification (UNNS)

δ can be treated as a boundary object: it marks the limit of compression, where residue variation becomes large and κ rises beyond Λ.

This is why δ appears constantly in physics notation (sources, impulses, Green functions): it is an encoded boundary, not a stable runtime survivor.

2) UNNS runtime scaffold: Sobtra → residue → curvature κ → admissibility

The Foundations Chamber implements a minimal but explicit runtime pipeline: generate a state series, apply Sobtra threshold clamping, compute residue, then compute a stability proxy κ and classify steps by Λ. The point is not “one model”; the point is an observable structure: κ defines regimes.

Operational scaffold (used for τ-filtered observability)
Generator: xn+1 = xn + δ + εn
Sobtra clamp: sn = xn if |xn| < θ, else 0
Residue: rn = xn − sn
Curvature: κn = |rn+1 − rn| / (|xn| + 10−9)
Admissible step: κn ≤ Λ
δ-as-distribution is defined in analysis by its action on test functions. δ-as-dynamic-state would correspond to forcing extreme concentration, which typically pushes κ upward and triggers inadmissibility. UNNS keeps both statements compatible by assigning them to different layers: definition layer vs survival layer.
Two layers: δ as definition vs δ as runtime state Definition Layer (Analysis) δ is a rule on a test space ∫ f(x) δ(x−a) dx = f(a) Stable as a mapping (well-defined action) No κ/Λ requirement at this layer Survival Layer (Dynamics) A state must remain τ-admissible κn = |rn+1 − rn| / (|xn| + 10−9) Admissible iff κn ≤ Λ reinterpret as a runtime target δ-like localization → κ rises → XII UNNS resolves the apparent conflict by assigning δ to two different roles: definition-object vs boundary-state.

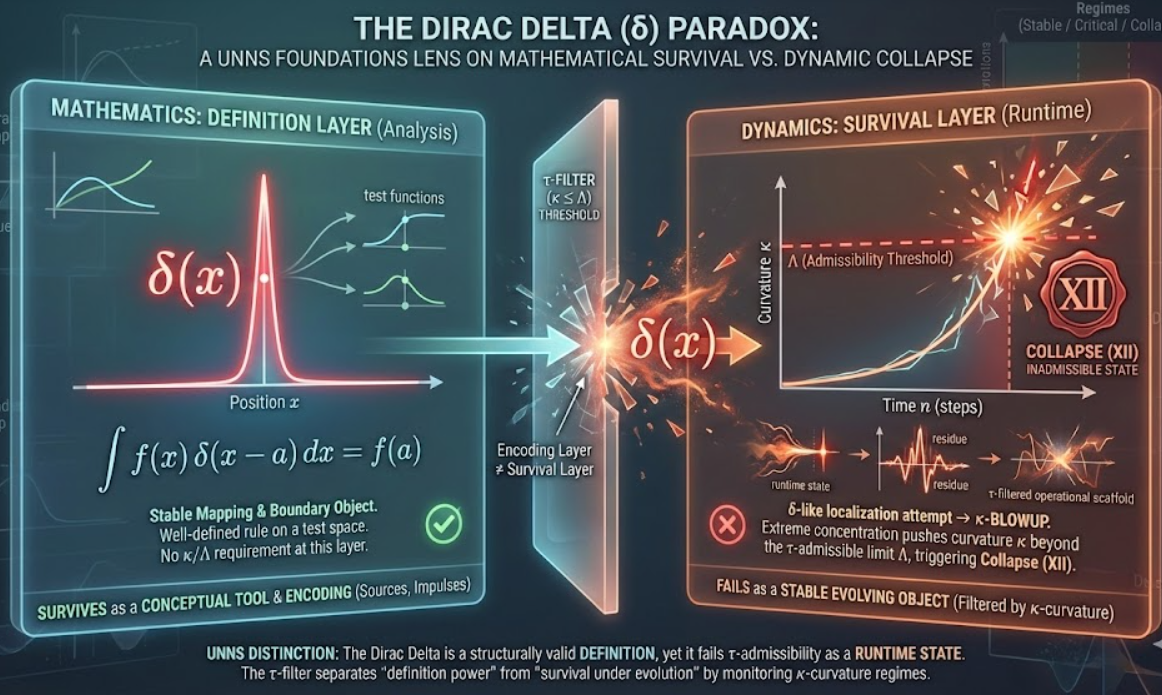
Figure A. δ is stable as a definition (mapping), but δ-like localization as a runtime target typically pushes κ above Λ and is classified as collapse-selected (XII).

3) Why δ fails in dynamics: κ blow-up and regime classification

A δ-like configuration concentrates “mass” into a narrow region. In a τ-filtered runtime, this tends to create large residue changes across steps, which increases |rn+1 − rn| and therefore increases κ. When κ exceeds Λ, the step is classified as inadmissible and labeled by Collapse (XII).

Curvature κ and τ-admissibility threshold Λ n (step) κ κ > Λ → collapse-selected region (XII) κ ≤ Λ → τ-admissible region Λ δ-like localization attempt κ rises above Λ

Figure B. A δ-like compression event is represented as a κ surge. The τ-filter turns “allowed / not allowed” into an observable regime: admissible steps satisfy κ ≤ Λ; steps above Λ are classified as collapse-selected (XII).

Stable regime

κ ≤ Λ for most steps; operator chains remain composable under τ-filtering.

Critical regime

κ frequently approaches Λ; small parameter shifts change survivability outcomes.

Collapse-dominated regime

κ exceeds Λ repeatedly; Collapse (XII) becomes frequent and truncates composition.

4) Why δ still “works” in physics notation

Physics uses δ to represent idealized sources, impulses, and point-like constraints. In UNNS terms, this is an encoding choice: δ is a compact symbol for a boundary condition, not a claim that a δ-state survives as a τ-admissible trajectory.

δ in physics: compact source encoding vs τ-admissible evolution Encoding Layer Impulse / point-source shorthand J(x) = J₀ δ(x − a) Used to define boundary forcing Not asserting a stable δ trajectory Survival Layer Evolve under τ-filtering admissible XII δ-like forcing can be modeled but δ-state itself is boundary-extreme apply forcing → test survival

Figure C. δ is frequently used as a compact way to encode forcing (sources, impulses). UNNS keeps that utility, then evaluates whether the resulting evolution remains τ-admissible. The “encoding layer” and “survival layer” are not the same claim.

5) Connection to quantum uncertainty: stability across dual descriptions

In quantum mechanics, sharp localization in one description corresponds to broad spread in a dual description (Fourier duality). UNNS reads this as a stability principle: pushing toward δ-like localization increases tension elsewhere and tends to raise κ under the τ-filter. The uncertainty bound is then read as a survival constraint across coupled channels, not a requirement to instantiate δ as a physical state.

Dual descriptions: localization tradeoff as a survival constraint Channel A (position-like) narrowing → δ-like tendency extreme localization → κ pressure Channel B (frequency-like) dual spread increases spread ↑ keeps product bounded Φ–Ψ duality coupling Runtime reading: pushing δ-like localization in one channel increases instability elsewhere → τ-filter enforces a survivable band.

Figure D. The δ-limit corresponds to extreme localization. Under a coupled dual description, that extremity pushes stress into the other channel. UNNS treats the familiar “uncertainty” pattern as a stability band that supports τ-admissible evolution across coupled views.

6) Try it live: Regime Lens (Figure B as a module)

If you want Figure B to be a live instrument (not a static sketch), embed a regime viewer that renders κ and Λ, and highlights stable / critical / collapse regimes as you tune Λ.

Open Regime Lens in a new window

Live Figure B. A τ-filter regime lens: κ profile + Λ threshold + regime classification. (If your Joomla editor strips iframes, place this inside a custom HTML module with iframe allowed.)

Conclusion

The Dirac delta survives in mathematics because it is defined as an action (a rule on test functions). It fails as a dynamic state because δ-like localization typically drives κ above Λ, which the τ-filter classifies as inadmissible, producing collapse-selected steps (XII). UNNS keeps both facts simultaneously by separating the definition layer from the survival layer, and by turning “allowed” into a measurable regime.

Takeaway (one line)

δ is a valid boundary definition, while δ-like runtime states are regime-extreme and are typically filtered by τ-admissibility (κ ≤ Λ) and Collapse (XII).

Resources

Foundations context and the executable instrument used for κ/Λ regime classification:

Main Menu