Recursive Survivability as the Defining Criterion of Mathematical Existence in the UNNS Substrate

How recursive survivability defines mathematical existence in the UNNS substrate

In our earlier research article UNNS and the Ontology of Mathematical Existence, we examined longstanding philosophical questions about what it means for mathematical entities to “exist”, and how different ontological positions grapple with that status (e.g., platonism, structuralism, nominalism).philpapers.org

Here we extend those reflections with a concrete artifact: the UNNS Operator Registry, the canonical Phase-B realization of the UNNS substrate.

From Ontology to Admissibility

Philosophers of mathematics have long debated whether mathematical entities — numbers, functions, sets — have objective existence, or whether their “existence” is merely a by-product of language or cognition.Wikipedia

The UNNS project approaches this from a different angle. Rather than asking whether mathematical objects exist, we ask:

Under what conditions does a recursive structure persist as a distinct, survivable entity?

This shifts the question from passive existence to recursive admissibility — a dynamic criterion grounded in recursion and structural invariance.

UNNS Substrate as Admissibility Substrate

In classical ontology, a substrate is what underlies all entities. In contrast, the UNNS substrate is not a universal domain of everything conceivable. Rather:

The UNNS substrate underlies only those recursive structures that survive recursive collapse.

This idea is central to the Operator Registry.

In Phase-A, we developed the generative foundations of recursion (Φ, Ψ, τ) and introduced Operator XII, the collapse operator that distinguishes survivable from non-survivable patterns.

In Phase-B, the Operator Registry makes this distinction explicit and comprehensive.

Operator XII and τ-MSC: Defining Survivability

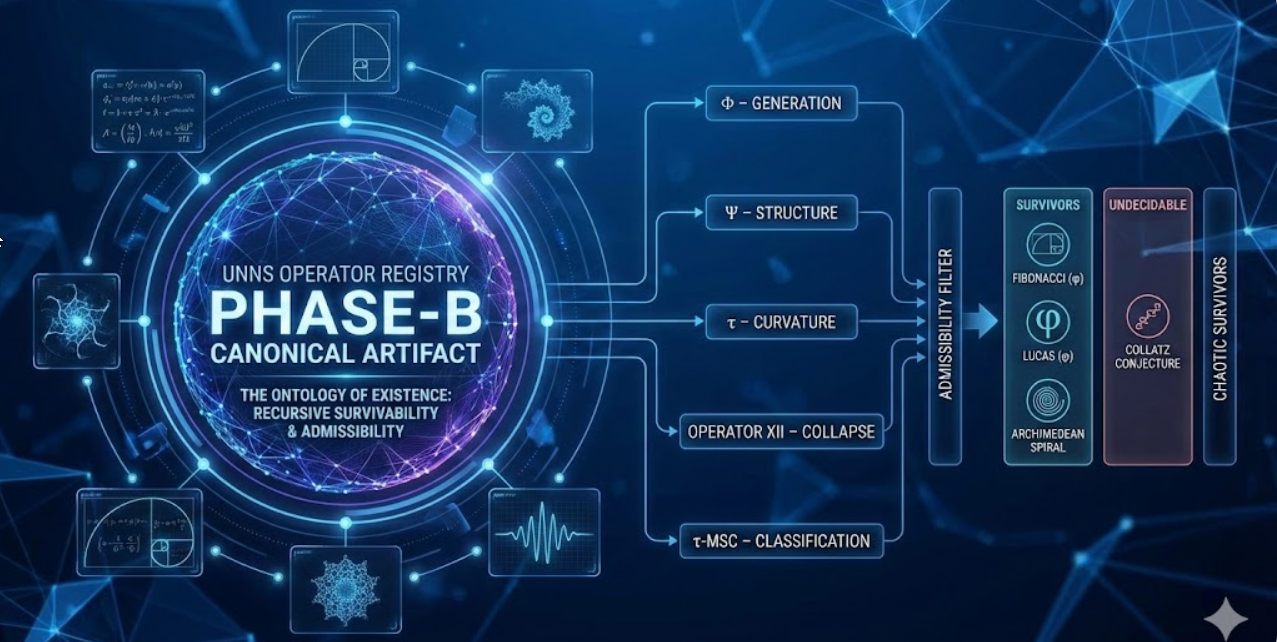
Every system in the Registry is classified through a structured pipeline:

1. Φ – Generation: the recursion rule that creates structure

2. Ψ – Structure: the invariant or emergent form

3. τ – Curvature: the recursive stability profile

4. Operator XII – Collapse: the admissibility filter

5. τ-MSC – Classification: the post-collapse status

Only systems that are interpretable through all five stages are included in the canonical Registry.

Some systems collapse to fixed invariants (e.g., the golden ratio in Fibonacci), some collapse into cycles or chaotic attractors, and some remain undecidable under current structural criteria.

Others — such as the Archimedean spiral — are structurally admissible without collapse, forming a distinct category of non-collapsing survivors.

This taxonomy is not about computational behavior, but about which structures are coherently present in the UNNS substrate.

Why This Matters for Existence

Where traditional ontologies ask whether abstract entities “exist”, UNNS asks:

Is this structure admissible under recursive survivability?

Admissibility is not about presence in reality, nor about mental representation. It is about structural coherence under infinite recursive pressure.

This position is neither platonist nor nominalist in the classical sense:

• It does not posit an abstract realm of all mathematical objects as inherently existing.iep.utm.edu

• It also does not reduce existence to linguistic convention or social construction.

Instead, UNNS asserts:

Existence — within the UNNS substrate — is determined by survivability under recursive collapse.

That is a clear ontological criterion.

The Registry as Canonical Artifact

The UNNS Operator Registry is now designated as Phase-B canonical. It is not an experiment, not a simulator, and not a demonstration. It is a declarative map of recursive admissibility.

Each entry in the Registry is a recursion class paired with a collapse signature.
Multiple systems may share the same signature, reflecting deep structural equivalence under infinite recursion.

This is not a “signature of everything” — it is a signature of what endures.

The Registry defines the substrate rather than imposing external criteria.

Relation to the Earlier Ontology Article

Our earlier article explored philosophical approaches to mathematical existence, including debates about abstract objecthood and structural realism.philpapers.org The Operator Registry now operationalizes a third stance:

• Not everything exists ontologically in UNNS.

• Not nothing exists outside conceptual frameworks.

• But what survives recursive collapse is admissible — and that survival is the criterion of existence in the substrate.

This is subtly different from saying “mathematics exists independently of us.” It says:

Mathematical structures exist insofar as they are recursively survivable invariants — not merely because they are defined.

What This Means Practically

• Fibonacci and Lucas sequences share the same collapse signature (φ).

• The Collatz conjecture remains undecidable under current substrate criteria.

• Some systems are classifiable as chaotic survivors or geometric survivors rather than convergent.

• The Registry explicitly marks what is admissible, undecidable, non-collapsing, or structurally invariant.

This makes the Registry a semantic atlas for recursive existence — a formal bridge between mathematical ontology and recursive structure theory.

Conclusion

The UNNS Operator Registry is more than a taxonomy. It is:

• A declarative substrate artifact

• A criterion of admissibility

• A map of recursive survivability

• A bridge between ontology and structure

It reframes existence not as a metaphysical given, nor as a social construct, but as a structural condition under recursive collapse — an answer to when and how a mathematical pattern is admissible in the UNNS substrate.

This article builds on our work on the ontology of mathematical existence and places it in a formal, structured context that is now complete for Phase-B.