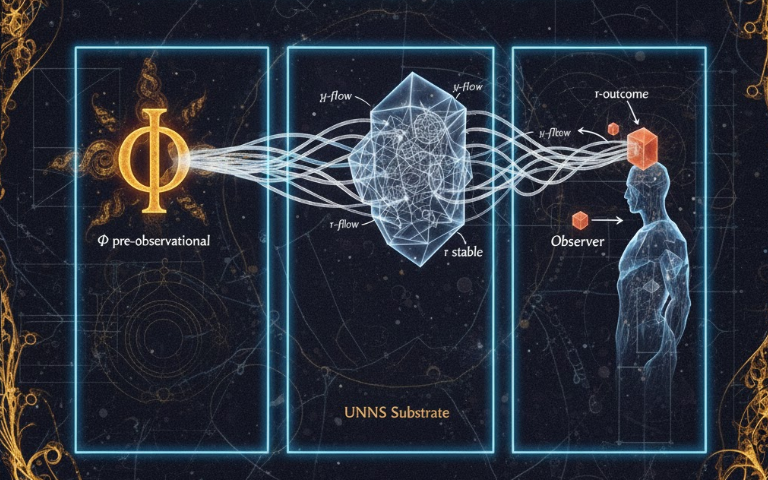
A UNNS Substrate Response to "Reality Exists Without Observers? Boooo!" (Nautilus)
A recent Nautilus article correctly dismantles popular myths about observers, consciousness, and quantum measurement. It rejects the idea that minds create reality, while also showing that attempts to banish observers entirely undermine empirical science.
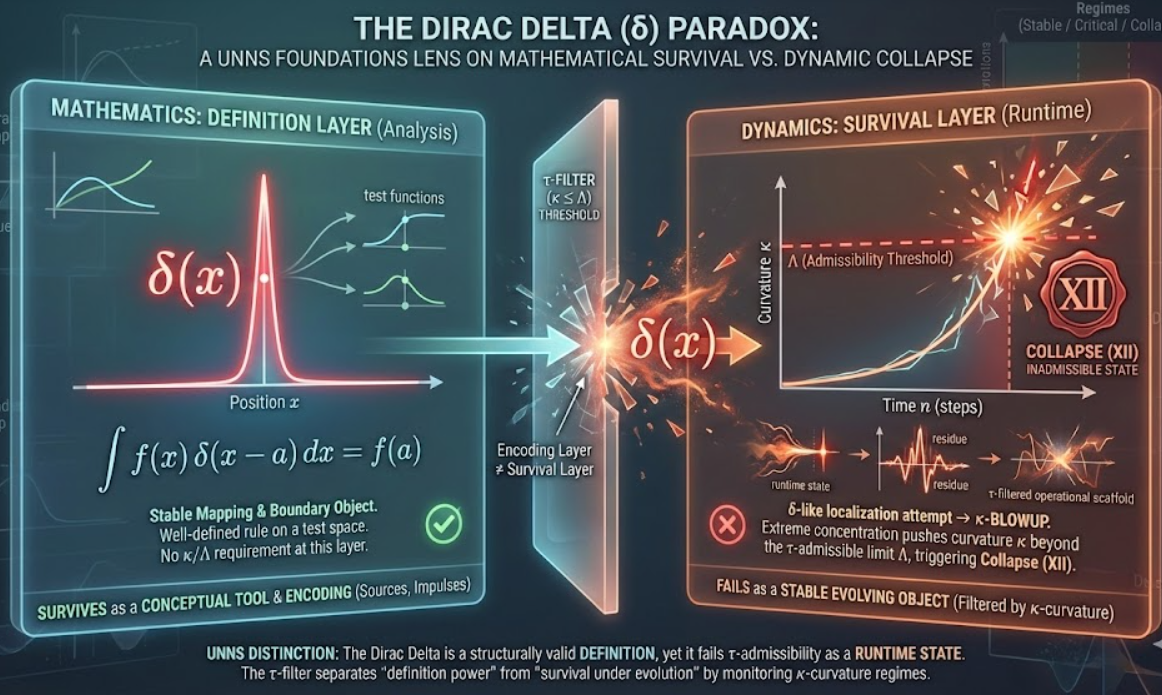
A UNNS foundations lens: δ(x) is structurally valid as a limit-object, yet it fails τ-admissibility as a runtime state. This article separates “definition power” from “survival under evolution” using κ-curvature, Λ thresholds, and Collapse (XII).
In classical analysis, δ is a distribution: it is defined by how it acts under integration against test functions. In dynamics, δ behaves like an “infinite localization” target. UNNS treats these as two different questions: What can be defined? versus What can survive as an evolving object?
Read more: Why the Dirac Delta Survives in Mathematics but Not in Dynamics
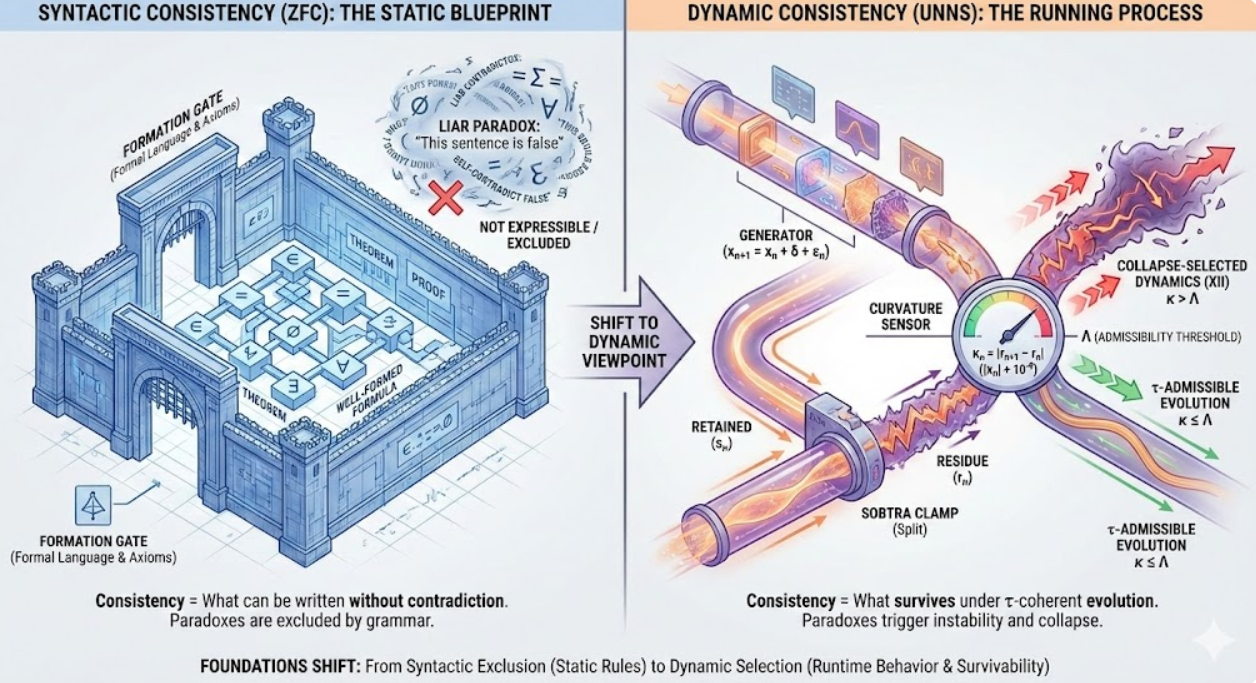
A public, operational viewpoint: what it means to be “consistent” when a mathematical universe is not only axioms, but a running process with admissibility, curvature, and collapse.
In classical set theory, “consistency” is largely a property of an axiom system and its formal language: what can be written, and what can be proved without contradiction. In UNNS, “consistency” is also a property of behavior: what survives under recursion, what remains admissible under τ-thresholds, and what collapses.
This article does not argue against ZFC. Instead, it clarifies a shift in viewpoint: syntactic exclusion versus dynamic selection. The two approaches can coexist — but they answer different questions.
Read more: From Syntactic Consistency (ZFC) to Dynamic Consistency (UNNS)
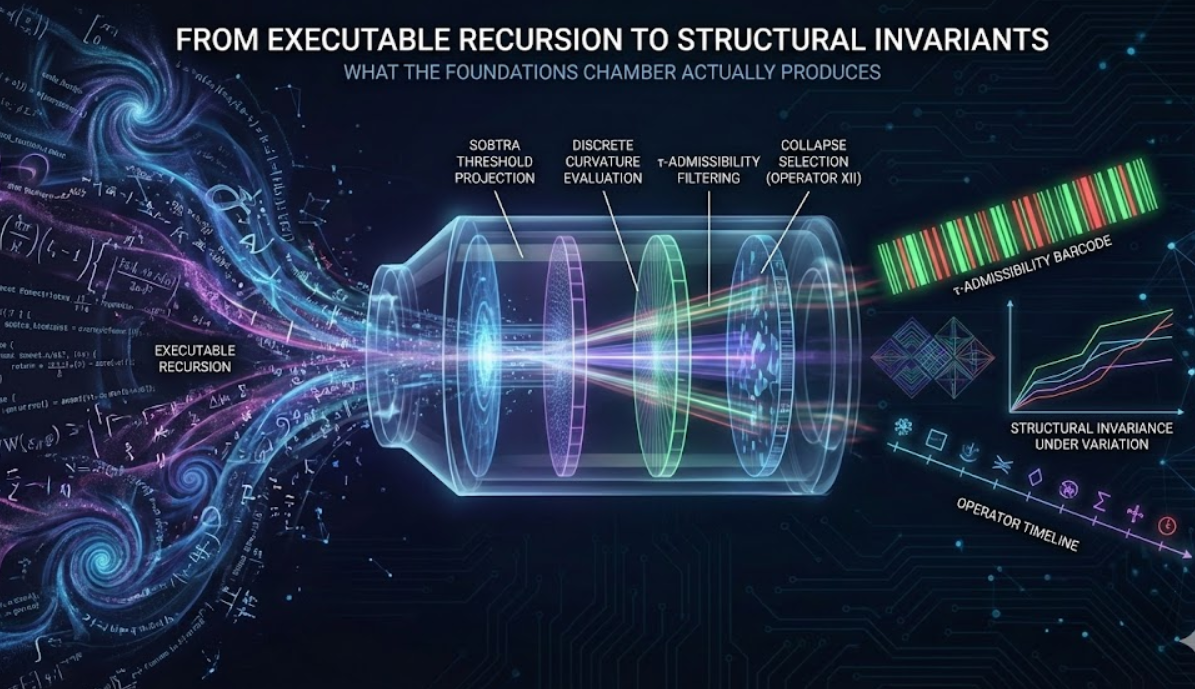
The UNNS τ-Filtered Observability — Foundations Chamber is not a visualization tool, nor a simulation in the conventional sense. It is an executable instrument designed to extract structural invariants from recursive dynamics under observability constraints.
This article clarifies what kind of results the Chamber produces, how they should be interpreted, and why they are neither numerical constants nor empirical predictions. Instead, the Chamber exposes relations that persist under controlled variation—the defining feature of structural invariants in mathematics and physics alike.
Read more: From Executable Recursion to Structural Invariants