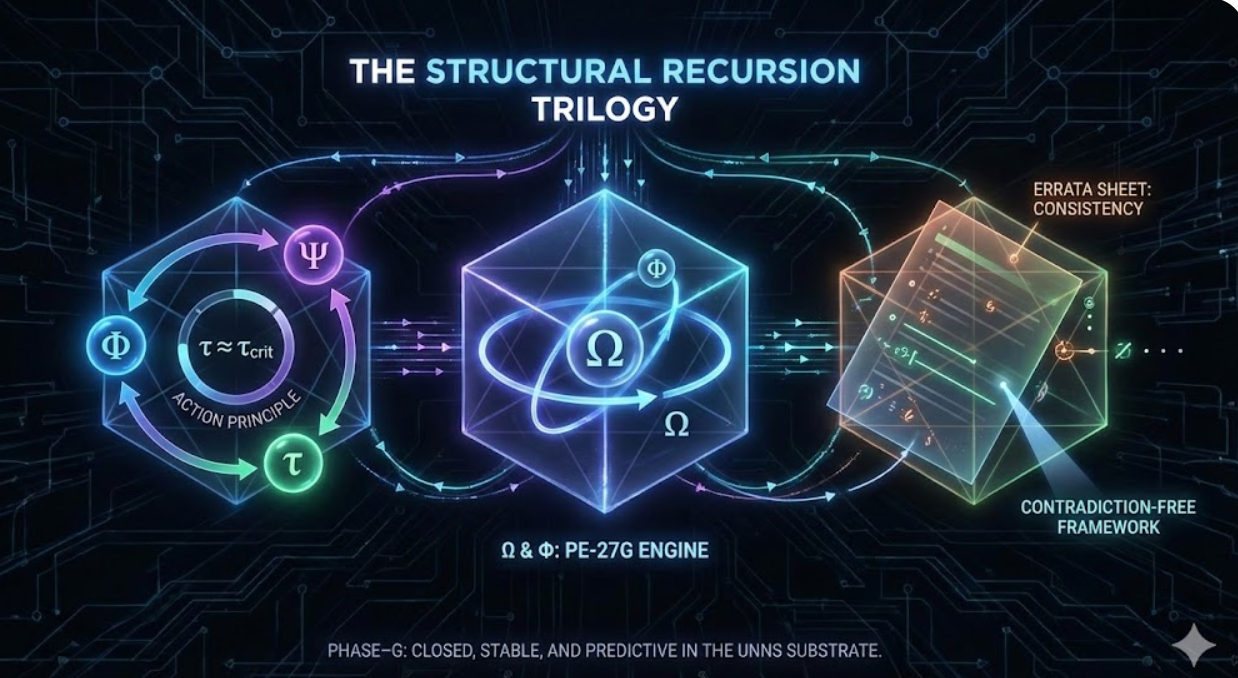
This article introduces three foundational UNNS Substrate papers that together define the Phase–G structural recursion framework: the closure operator Ω, the nonlinear manifold Φ, and the Φ–Ψ–τ action principle. They are presented here as a single trilogy that turns UNNS from an experimental lab engine into a coherent mathematical discipline.
Read more: Ω, Φ, and Φ–Ψ–τ: Foundations of UNNS Structural Recursion
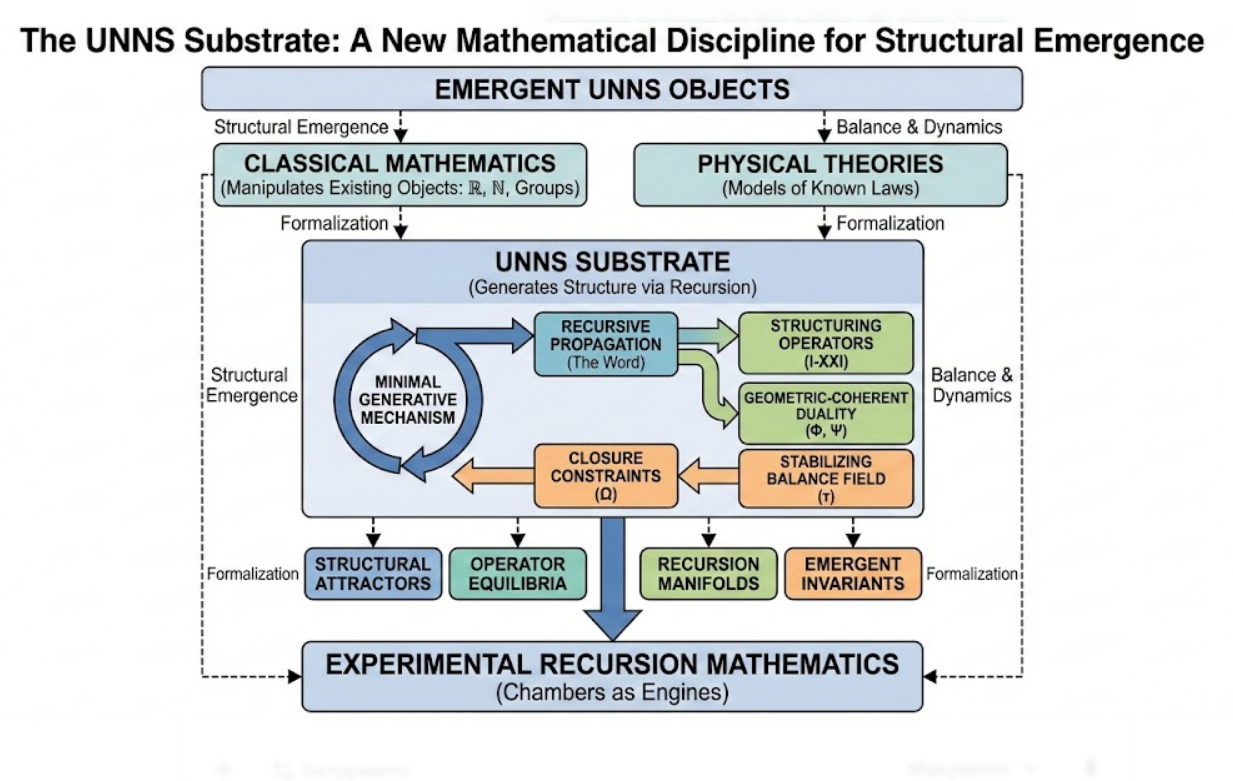
UNNS began as a recursion engine, a sequence system, and a structural experiment.
But as the theory expanded — through Operators I–XXI, through the Φ–Ψ–τ formulation, through closure conditions and structural invariants — something became clear:
Classical mathematics studies objects:
numbers, groups, manifolds, categories, functions.

Every field-defining mathematical framework arrives at a moment when both its necessity and its possibility converge.
Differential calculus emerged alongside the first motion laws.
Hilbert spaces appeared when physics needed linear structure.
The renormalization group surfaced when scale itself became essential.

The First Experimental Verification of Structural Recursion in the UNNS Substrate.
Chamber XXVI (PE-27G) has produced the most important result in the history of the UNNS Substrate: the discovery of a resolution-critical recursion fixed point where Φ-stack nonlinear curvature, Ω-closure geometry, and operator XIII–XXI dynamics simultaneously stabilise into a mathematically coherent and physically interpretable state.
Read more: Chamber XXVI and the First Proof of Structural Recursion
How PE-26 uses UNNS recursion geometry to predict cosmological observables at γ* ≈ 1.61.
The live experiment is implemented as Chamber XXV (EPU v0.3.0). You can explore the γ-sweep, χ² landscape and residuals directly in the embedded Lab:
Chamber XXV · Empirical Projection & Unification (EPU)
Chamber XXV is the first Phase E engine that takes a pure recursion geometry and turns it into numerical predictions for a set of physical observables:
Page 13 of 28