
Foundations → Recursion & Stability UNNS Lab — Chamber Logic Classical vs UNNS
There are mathematical examples that are trivial in appearance yet structurally revelatory. The Fibonacci sequence is one of them. It has been dissected, analyzed, celebrated, and mythologized for centuries. But what happens when we view it through the UNNS Substrate — a framework that treats recursion not as algebraic coincidence but as a physical flow of echo amplitudes through a computational medium?
This article is a bridge between worlds. It takes a universally familiar mathematical object, the weighted Fibonacci series
S = ∑n=0∞ Fn / 2n,
and shows how two different intellectual traditions — classical analysis and UNNS recursion theory — arrive at the same number but through radically different ontologies. One sees algebraic cancellation; the other sees structural equilibrium. One explains how the sum is computed; the other explains why the sum could not have been anything else.
For the shifted Fibonacci sequence (1,1,2,3,5,...), the sum equals:
S = 4.
Read more: Comparative Study: Fibonacci Series in Classical Analysis and UNNS Substrate

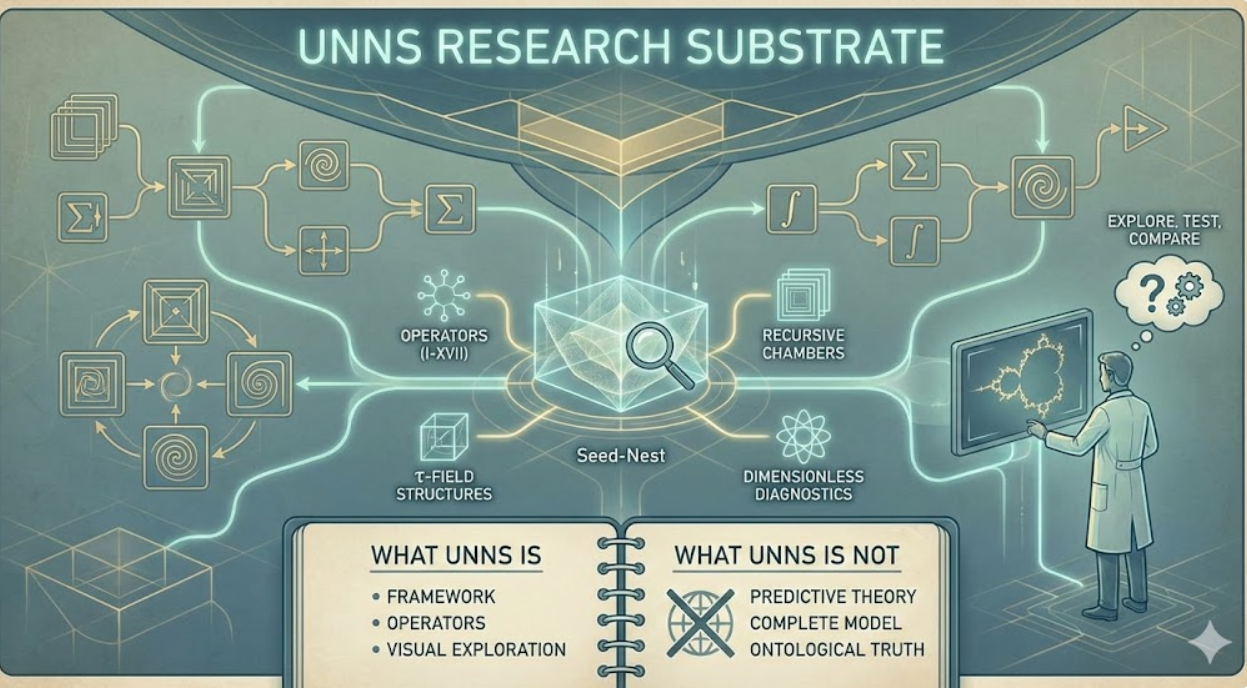
Foundations Research Substrate UNNS Philosophy
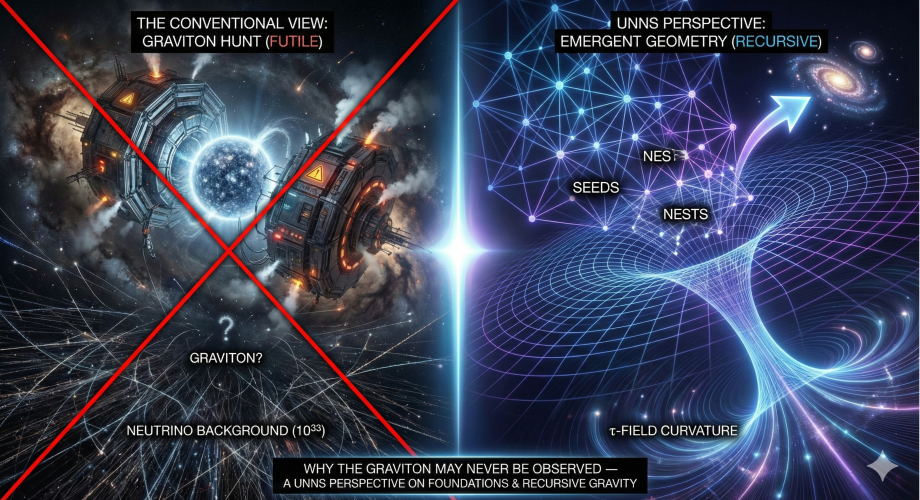
Foundations τ-Field Recursive Gravity
Read more: Why the Graviton May Never Be Observed — A UNNS Perspective

Foundations Seed ↦ Nest Observer Dynamics
Page 16 of 28