
The UNNS Substrate begins with a simple premise:
structure precedes interpretation.
Before equations describe forces, before geometry becomes spacetime, before probability becomes prediction, there exists a deeper layer of organization — a recursive substrate from which formal structures can be constructed, projected, and tested for stability.
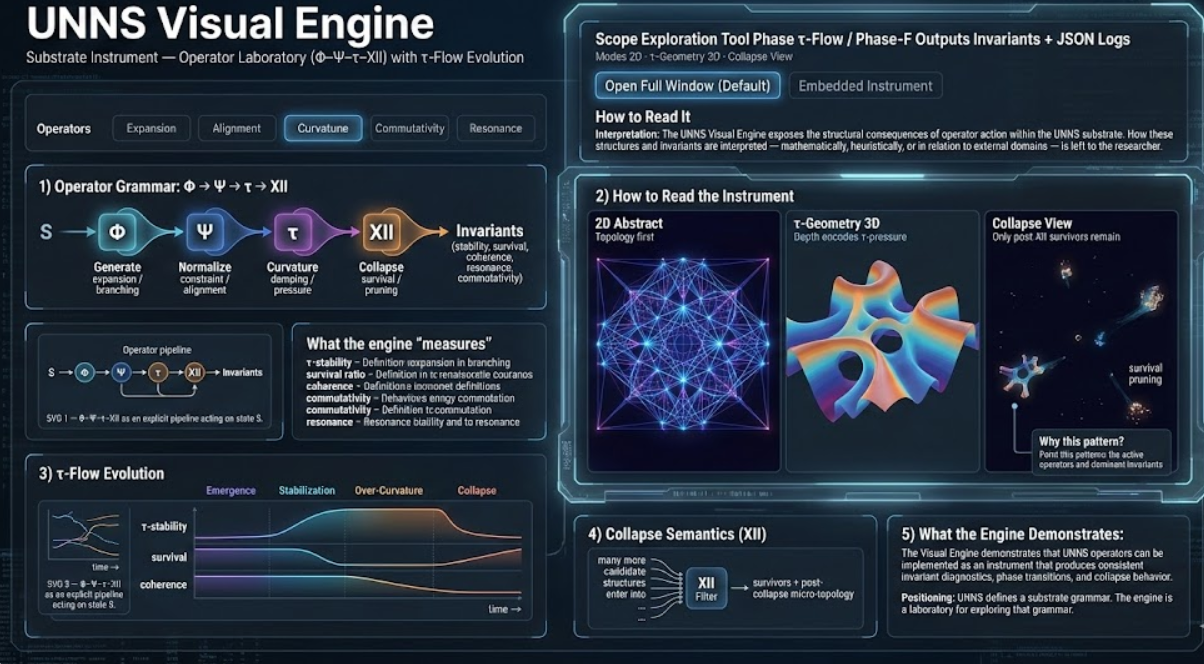
Substrate Instrument — Operator Laboratory (Φ–Ψ–τ–XII) with τ-Flow Evolution

Phase-C Exploratory Chamber — a pre-collapse microscope for observing how symbolic structures behave under recursive and geometric transformations.
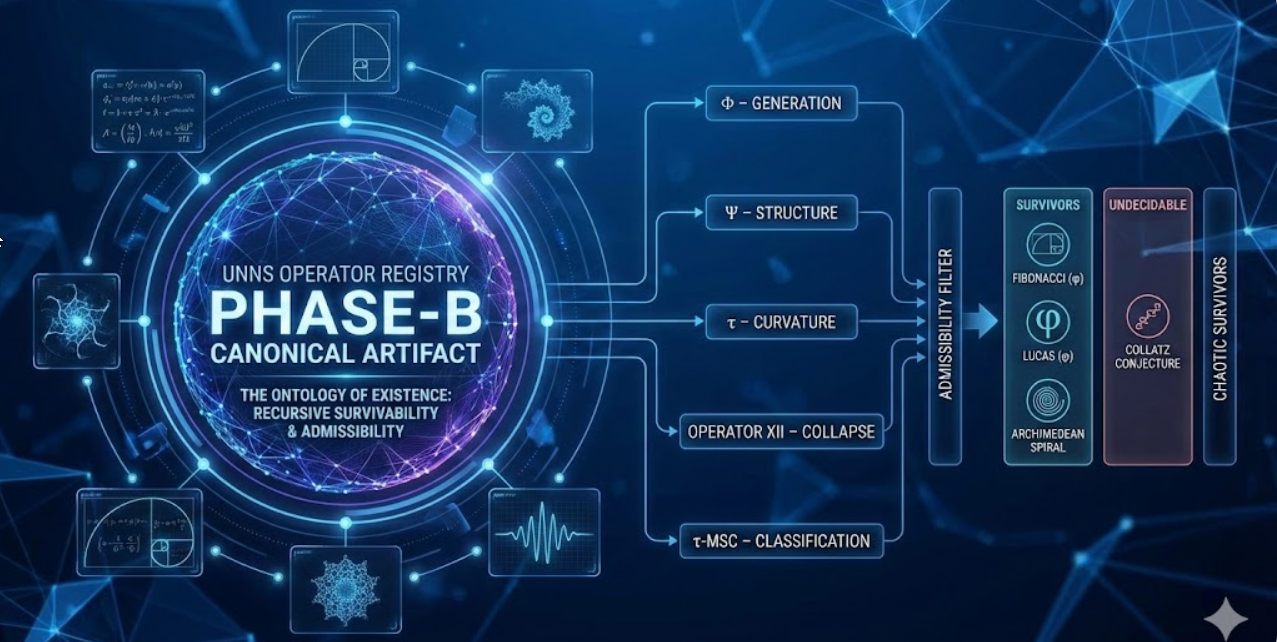
How recursive survivability defines mathematical existence in the UNNS substrate
In our earlier research article UNNS and the Ontology of Mathematical Existence, we examined longstanding philosophical questions about what it means for mathematical entities to “exist”, and how different ontological positions grapple with that status (e.g., platonism, structuralism, nominalism).philpapers.org
Here we extend those reflections with a concrete artifact: the UNNS Operator Registry, the canonical Phase-B realization of the UNNS substrate.
Read more: UNNS Phase-B: The Operator Registry and the Ontology of Existence

UNNS-Tech Applied to Quantum Mechanics
We reinterpret the Born rule — the prescription that the squared magnitude of a wavefunction yields observable “probability” — not as a foundational probability axiom but as the unique surviving invariant under a sequence of UNNS operators. Within the UNNS substrate, ψ itself is a generable recursive structure (Φ-stage). Through structural consistency (Ψ) and curvature stability (τ), |ψ|² emerges as the sole post-collapse invariant admissible under collapse operator XII. This reframes Born’s rule as a consequence of recursive stability and measurement collapse, aligning it directly with outcomes in Chamber XXVI and Chamber XXVIII.
Read more: Born’s Rule as a Structural Invariant, Not a Probability Postulate
Page 11 of 28